| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
- 라우터
- container
- mybatis
- Spring
- Set
- Java
- STREAM
- DevOps
- post
- Jenkins
- Linux
- Pipeline
- 허브
- LAN어댑터
- map
- AOP
- gradle
- 소켓
- cloud
- docker
- IntelliJ
- ansible
- 액세스회선
- tomcat
- 캐시서버
- Collection
- 방화벽
- JPA
- sonarQube
- jdk
- Today
- Total
거북이-https://velog.io/@violet_evgadn 이전완료
log & 거듭제곱 본문
코딩 테스트 시 필요한 이유
사실 코딩 테스트 때 로그는 그렇게까지 중요도가 높지는 않다. 즉, 사용하지 않아도 문제를 풀 수 있다.
하지만 필자는 자릿수를 구하는 문제이거나 규칙을 가진 상황에서 특정 값의 Index를 구하는 종류의 문제들은 주로 log를 활용한다.
굳이 이렇게 풀지 않아도 되지만 수학을 좋아했던 예전 기억이 남아 있어서 이런 게 아닐까 싶다.
어차피 활용할 거 제대로 한 번 정리해보자고 결정했고, 이왕 정리하는 거 log의 반대 성질을 가진 거듭제곱까지 한 번에 정리하기로 하였다.
Math.log
Java에서 log를 사용하는 방법은 총 3가지 존재한다.
밑이 e(자연 상수)인 ln(x) 값을 반환하는 Math.log(x), 밑이 10인 log(x) 값을 반환하는 Math.log10(x), 마지막으로 ln(x+1) 값을 반환하는 Math.log1p(x)이다.
실제로 각 메서드가 위에서 기입한 함수 결과를 반환하는지 코드를 통해 확인해보자.
(참고로 자연 상수 e는 Math.E로 사용할 수 있다)
System.out.println("[Math.log는 ln(x)일까?]");
System.out.println(Math.log(Math.E)==1? "맞다" : "틀리다");
System.out.println("[Math.log10은 log10(x)일까?]");
System.out.println(Math.log10(10)==1? "맞다" : "틀리다");
System.out.println("[Math.log1p는 ln(x+1)일까?]");
System.out.println(Math.log1p(Math.E-1)==1? "맞다" : "틀리다");
이렇게 3가지 방법이 존재하지만 사실 Math.log()만 알고 있으면 된다.
그 이유는 수학 공식에는 "로그의 밑변환 공식"이라는 수식이 존재하기 때문이다.

위 이미지가 로그의 밑변환 공식인데 이를 사용하면 Math.log()만 사용해도 모든 log 함수를 만들 수 있다.
예를 들어 밑이 2인 로그 log₂(x)를 구하고 싶을 경우 ln(x)/ln(2)를 수행하면 되므로 Math.log(x)/Math.log(2)를 통해 구할 수 있다.
이를 확장시키면 밑이 r인 로그 logᵣ(x)를 구하고 싶을 경우 Math.log(x)/Math.log(r)을 계산하면 구할 수 있게 되는 것이다.
따라서 log 관련 모든 함수를 외우지 말고 Math.log()와 로그의 밑변환 공식을 활용하자.
◎ 주의할 점!!!!!!
Math.log를 사용할 떄 주의할 점이 있다.
바로 Math.log(0)이 안되도록 주의할 것!
알다시피 log 함수는 진수로 0 값이 들어올 수 없다.
마찬가지로 Math.log(0)으로 ln(0)을 만들어버린다면 계산상 오류가 발생할 수 있으므로 0 값이 주입되지 않도록 주의하자.
Math.pow
Java에서 거듭제곱은 Math.pow 함수를 활용한다.
Math.pow(double x, double y) // x^yMath.pow(double a, double b) 메서드는 aᵇ 결괏값을 반환한다.
이때 알아야 하는 것은 Parmeter인 a와 b의 자료형은 double이고, Math.pow() 결괏값 또한 double 자료형을 가진다는 것이다.
이런 특징 때문에 a 거듭제곱을 수행할 때 a*a*...*a 연산을 수행하는 것보다는 Math.pow() 활용을 추천한다.
코드를 통해 왜 Math.pow()를 추천하는지 알아보자.
int a = Integer.MAX_VALUE/2;
System.out.println(a*a);
System.out.println(Math.pow(a,2));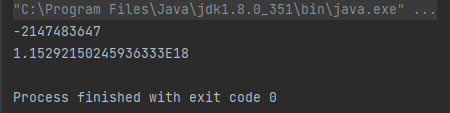
직접 a*a를 수행했을 경우 Overflow 때문에 음수 & 부정확한 연산 결과가 도출되었다.
하지만 Math.pow(a,2)를 통해 거듭제곱을 수행했을 경우 정확한 곱연산 결과가 도출되었음을 확인할 수 있다.
Math.pow()는 double 자료형으로 결괏값을 처리하는데 double 자료형은 8 Byte 공간으로 데이터를 처리한다.
즉, 4 Byte를 활용하는 int 자료형보다 더 많은 범위의 수를 나타낼 수 있게 되는 것이다.
거듭제곱은 알다시피 연산의 결과증가폭이 기하급수적으로 증가하므로 최대한 넓은 범위를 처리할 수 있는 Math.pow() 연산 사용을 추천하는 것이다.
'코딩 테스트 시 알면 좋은 것들' 카테고리의 다른 글
| 문자열 뒤집기 (0) | 2023.01.03 |
|---|---|
| Compare 관련 메소드 (0) | 2022.12.31 |
| N 진법 (0) | 2022.12.30 |
| Long & Int 범위 (0) | 2022.12.30 |
| Stream을 활용한 Collection to Array & Array to Collection (0) | 2022.12.30 |




